● 본 공부와 기록은 유튜버 '노마드 코더 Nomad Coders' 님의 "어? 재밌네? 정렬 알고리즘, 한방에 이해하기!"을 기본으로 하였다.
→ https://www.youtube.com/watch?v=Bor_CRWEIXo&list=PL7jH19IHhOLMdHvl3KBfFI70r9P0lkJwL&index=6
☆ Big O의 예외

→ Big O는 알고리즘의 퍼포먼스를 이해하기 쉽고 효율적으로 작성하는 방법이다.
→ 그러나 Big O가 모든 알고리즘을 완벽하게 설명하는 건 아니다.
→ 이제 설명할 알고리즘들은 같은 Big O를 가지고 있지만, 각각의 퍼포먼스가 매우 다르다.
☆ Sorting
→ Sorting은 뭔가를 정리하는 것이다.
→ 사전처럼 A~Z로 정렬하든가, 큰 수에서 작은 수 기준으로 정렬할 수도 있다.
→ 이진검색처럼 빠른 알고리즘을 사용하려면 먼저 배열을 정렬해야한다.
- 버블 정렬 Bubble Sort
- 선택 정렬 Selection Sort
- 삽입 정렬 Insertion Sort
→ 물론, 이것들이 가장 빠른 정렬 알고리즘은 아니다.
→ 그러나 실제로 사람들이 정렬하는 방법과 매우 유사하다.
→ 시간 복잡도를 계산하는 방법도 쉽다.
★ 버블 정렬 Bubble Sort O(n^2)
→ 버블 정렬은 그렇게 좋은 알고리즘은 아니기에 자주 사용되지는 않는다.
→ 그 대신 정렬 알고리즘 입문으로는 이해가 쉽다.

① 배열의 두 개의 아이템을 선택하고, 비교한다.
② 왼쪽이 오른쪽보다 크면 교환한다.
→ 5는 2보다 크니까 교환한다.

③ 오른쪽으로 이동해서 해당 프로세스를 반복한다.
→ 5는 6보다 작기에 교환하지 않는다.

④ 다음 대상으로 이동한다.
→ 이번엔 6이 3보다 큰지 비교하고, 크기때문에 스왑한다.

→ 6과 1을 비교하고 교체한다.
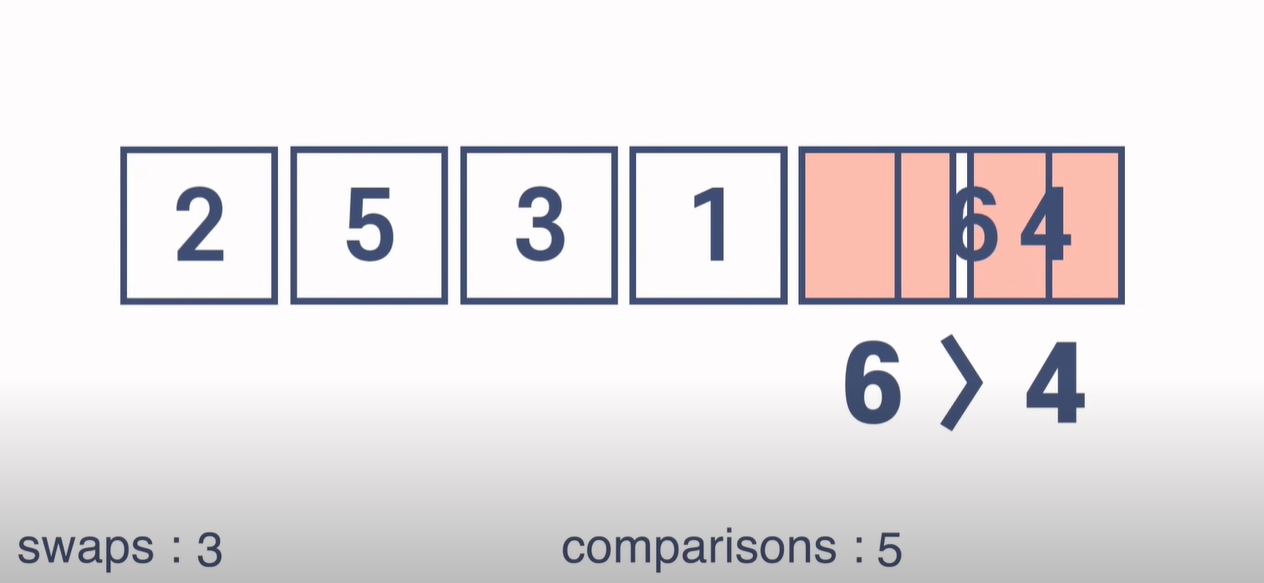
→ 6과 4를 비교하여 교체한다.
→ 큰 아이템이 끝까지 '버블'로 이동하니까 버블 솔트라 불리는 것이다.
→ 총 결과 값은 아래와 같다.

→ 그렇다면 버블 정렬의 시간 복잡도는 무엇일까?

→ 이걸 알기 위해서는 배열의 N-1, N-2, N-3...의 아이템과 비교해야한다.
→ 아이템이 6개라면, 5번 비교해야한다.
→ 최악의 경우엔 모든 싸이클마다 모든 아이템을 스왑해야 한다.
→ 요컨대 내가 가지고 있던 정렬이 내림차순인 경우다.
→ 따라서 버블 정렬의 시간복잡도는 O(n^2)이다.
★ 선택 정렬 Selection Sort O(n^2)

→ 아까와 같은 예시를 통해 비교해보자.
→ 전체 아이템 중에서 가장 작은 아이템의 위치를 변수에 저장한다.

→ '1' 보다 바로 크면서 다음으로 작은 '2'의 위치변수를 저장한다.
→ 계속 체크하다 '1'에 도착하면 해당 위치를 저장하고, 사이클을 끝낸다.

→ 이제 배열에서 가장 작은 숫자가 어디있는지 알고 있다.
→ 가장 작은 숫자와 첫번째 아이템과 바꾼다.

→ 다음 사이클을 시작할 때에는 '1'로 시작하지 않는다.
→ '1'은 정렬된 파트이므로, 다음은 정렬되지 않은 부분 중에서 가장 작은 숫자를 찾는다.
→ 이미 정렬된 '1'은 제외한다.

→ 그 다음으로 가장 작은 숫자인 '2'를 찾고, '2'는 이미 올바른 위치에 있으니 스왑하지 않는다.
→ 이렇게 작은 숫자 찾고 스왑하기를 반복하는 것이다.
→ 그럼 선택 정렬의 시간복잡도는 무엇일까?
→ 버블 정렬과 비슷하게 스왑과 비교가 모두 존재한다.
→ 정렬되지 않은 배열에서 가장 작은 숫자를 찾으므로, N-1과 비교하며, 이는 버블 정렬과 같다.
→ 그러나 최악의 경우, 버블 정렬과 달리 N번의 스왑을 하지 않는다.

→ 매 싸이클마다 1번만 스왑하면 된다.
→ 즉, 선택 정렬이 버블 정렬보다 훨씬 선호된다.
→ 선택 정렬이 버블 정렬보다 2배 더 빠를 수 있음에도 불구하고, 선택 정렬의 시간복잡도 역시 O(n^2)이다.
★ 삽입 정렬 Insertion Sort O(n^2)

ex) 동일한 예시로 인덱스 1번부터 시작해보자.
→ 왼쪽에 숫자 '2'보다 큰 숫자가 있는지 살펴본다.
→ 1 사이클

→ 그 경우, 5를 오른쪽으로 밀고 2는 왼쪽으로 이동한다.

→ 2 사이클
→ '6'을 선택하고, 왼쪽의 숫자가 더 큰지 비교한다.
→ 없는 경우, 계속 진행한다.

→ 3 사이클
→ '3'을 선택했고, '3'보다 왼쪽에 더 큰 숫자가 존재한다.
→ 따라서 '3'과 '6'을 교체하고, 다시 '3'과 '5'를 교체한다.
→ 그리고 '2'와 '3'을 비교했을 때, '3'이 더 작으므로 올바른 위치에 왔다고 말할 수 있다.

→ 4 사이클
→ '1'로도 동일한 작업을 반복한다.
→ 그 결과, 1이 맨 왼쪽에 가게 된다.
→ 5 사이클에서 '4'에 대해 동일한 작업을 실행하면 작업이 끝나게 된다.
→ 삽입 정렬 Insertion > 선택 정렬 Selection > 버블 정렬 Bubble 순으로 빠르며, 선호된다.
→ 삽입 정렬이 선택 정렬보다 빠르다.
→ 그 이유는 선택 정렬이 모든 아이템을 스캔하는데 반해, 삽입 정렬이 필요한 아이템만 스캔하기 때문이다.
→ 그러나 삽입 정렬이 선택 정렬보다 빨라도 시간복잡도는 동일하게 O(n^2)이다.
☆ 세 정렬의 시간복잡도가 동일한 이유
→ 앞서 살펴본 세 알고리즘은 매우 다른데도, 시간복잡도는 똑같았다.
→ 이 경우, 최악의 시나리오를 보지말고 '평균 시나리오'를 봐야한다.
→ 최악/최고의 케이스는 자주 발생하지 않고, 대부분은 평균에 속한다.

→ 이를 바탕으로 삽입 정렬, 선택 정렬을 살펴보면 평균적으로, 최악으로 모두 이차 시간복합도를 갖는다.
→ 그러나 보이는 바와 같이, 삽입 정렬에서 O(N)이 최고의 시나리오에서 발생한다.
→ 결국, 이렇게 동일한 시간복잡도를 가지고 있더라도 매우 다르게 나타날 수 있다는 점이다.
→ 삽입, 선택 정렬은 작은 DB 기준으로는 훌륭한 알고리즘이다.
→ 물론, 데이터가 커질수록 느려진다.
'프로그래밍 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 2021년 8월 20일 - Stack & Que (0) | 2021.08.20 |
|---|---|
| 2021년 8월 4일 - Big O (0) | 2021.08.04 |
| 2021년 8월 3일 - Binary & Linear (0) | 2021.08.03 |
| 2021년 8월 2일 - 배열 Array (0) | 2021.08.02 |
| 2021년 7월 30일 - 알고리즘을 공부해야하는 이유 (0) | 2021.07.30 |




댓글